ここでは,前編「openFrameworks 入門編(1)」に続いて,より高度なグラフィクス処理や C++ 特有のオブジェクト指向プログラミングについて説明していきます.
デフォルトの座標系は,左下図に示すように,画面の左上を原点 (0, 0) とする直交座標系で,横方向(右方向)が X 軸,縦方向(下方向)が Y 軸です.たとえば ofSetWindowShape(600, 400) とすれば,アプリケーションのウィンドウは,横(X 軸)が 600 ピクセル,縦(Y 軸)が 400 ピクセルとなります.

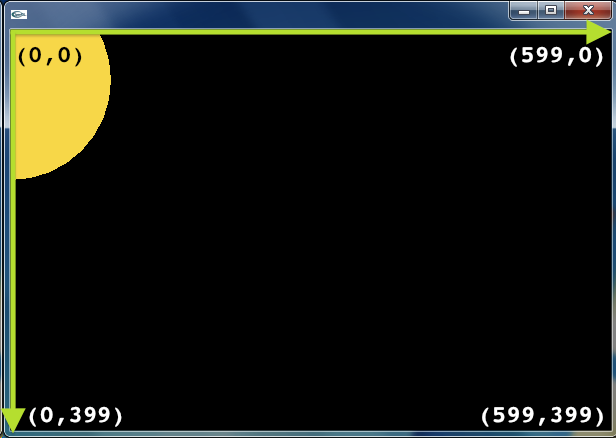
このデフォルト座標系で,原点にキーポンを描いてみましょう.emptyExample をコピーして dojoExample4 をつくり,ofApp.cpp を以下のように記述します.このプログラムを動かすと,右上図のように,キーポンの一部らしき黄色い丸がウィンドウ左上端に表示されるはずです.
#include "ofApp.h"
void ofApp::setup () {
// 600x400, 30 frames/sec
ofSetWindowShape(600, 400);
ofSetFrameRate(30);
ofSetCircleResolution(32);
// black background
ofSetBackgroundColor(0, 0, 0);
}
void ofApp::draw () {
// Keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
}
(... 以下変更なし ...)
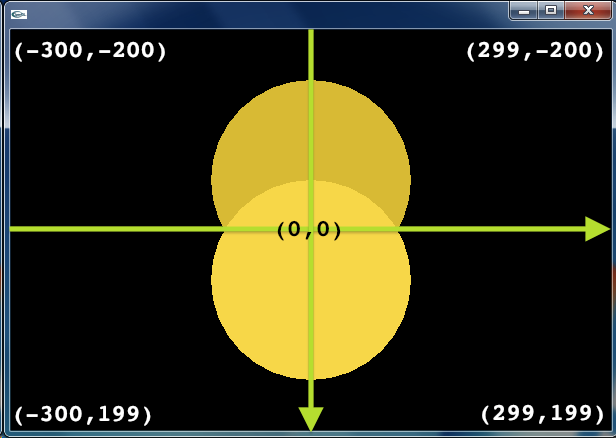
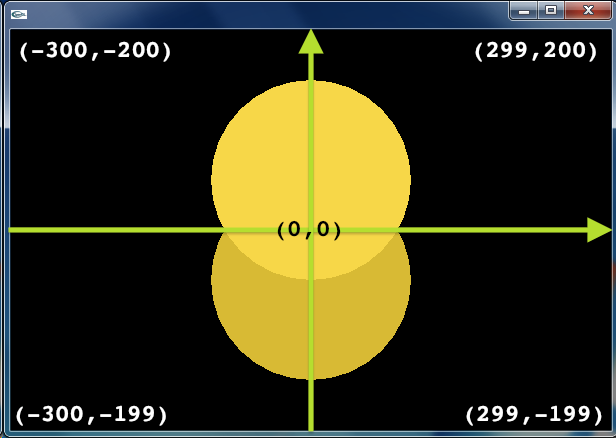
この座標系は使いづらいですね.原点に描いたものは,ウィンドウの真ん中に表示されて欲しいです.そこで,OpenGL や数学で使う標準的な座標系に変更することを考えます.下にあげたプログラムのように,ofApp::draw() の中で,まず ofTranslate(300, 200) によって,元の座標系を X 軸方向(右方向)に 300,Y 軸方向(下方向)に 200 だけ平行移動させると,左下図のような座標系が得られます.つぎに ofScale(1, −1) によって,Y 軸の向きを反転させることで,右下図のような標準的な座標系(いわゆる右手系)が得られます.これ以降描画される図形は,この新しい座標系の中に配置されるようになります.
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
}
発展課題1: 上の例では,ofScale(1, −1) とすることで,Y 軸の方向を反転させていましたが,本来 ofScale(sx, sy) は,X 軸を sx 倍に,Y 軸を sy 倍にすることで,座標系の拡大縮小(いわゆるスケール変換)を行なうものです.原点を中心とした拡大縮小となるため,原点は不動点(動かない点)となります.ofScale(2, 1) とすると,X 軸方向(横方向)に2倍に引き伸ばされ,真円を描いても画面上には横長の楕円として表示されます.ofScale(1, 1) は何の変化も与えません.つぎのプログラムを実行して,ofScale() の動作を確かめてください.
#pragma once
#include "ofMain.h"
class ofApp : public ofBaseApp {
private:
float rad;
public:
(... 変更なし ...)
};
#include "ofApp.h"
void ofApp::setup () {
// 600x400, 30 frames/sec
ofSetWindowShape(600, 400);
ofSetFrameRate(30);
ofSetCircleResolution(32);
ofSetBackgroundColor(0, 0, 0);
// init vars
rad = 0.0;
}
void ofApp::update () {
rad += 0.1;
}
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// boing boing
float sy = 0.9 + 0.1 * sin(rad);
ofScale(1, sy);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
}
発展課題2: 以下のように ofScale() に値を与えると,キーポンが回転するように見えます.なぜこうなるか考えてみてください.プログラムを少し変更して,横回転など,別パターンも試してみてください.
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// turning
float sy = sin(rad);
ofScale(1, sy);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
}
発展課題3: キーポンに,少しだけ「なまめかしい」動きを与えてみましょう.下のように ofApp::draw() を書き換えて動かしてみてください.
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// boing boing
float sy = 0.9 + 0.02 * sin(rad * 5);
float sx = 0.9 + 0.02 * cos(rad * 6);
ofScale(sx, sy);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
}
平行移動の ofTranslate() や拡大縮小の ofScale() は,いずれも座標系を変換する操作です.こうして得られた座標系を基準として,それ以降の図形の描画が行われます.
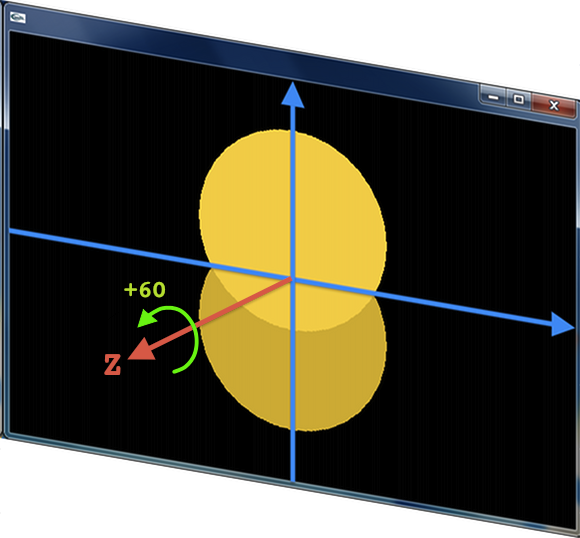
もうひとつ,大切な座標変換に回転があります.座標系を回転させるとは,原点から画面に垂直方向(手前側)に伸びた Z 軸まわりに XY 平面を回転させることです.現在の座標系を原点まわりに 60deg 回転させるには,下にあげた部分プログラムのように,ofRotateZ(60) を実行すればよいでしょう.なお回転の方向は,軸の正方向(矢印方向)に「右ネジ」を進めたときの回転方向が正となります.Z 軸を正回転させれば,XY 平面は原点を中心に反時計回りに回転します.
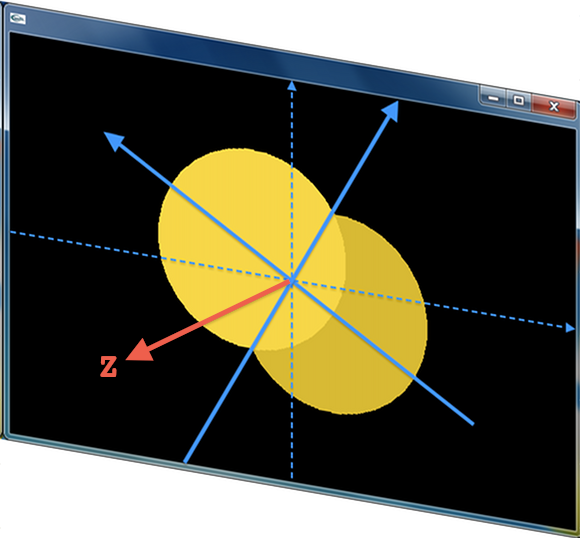
Z 軸まわりに 60deg 回転させた座標系(右図の青い実線)を基準として,キーポンを描けば,画面内のキーポンは反時計方向りに 60deg 傾くことになります.つぎにあげる ofApp::draw() を動かして,この動作を確かめてください.
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// rotate 60
ofRotateZ(60);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
}
発展課題1: キーポンに黒目を入れることを考えます.回転された座標系の中で,通常どおりの位置に黒目を描けばよいです.

void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// rotate 60
ofRotateZ(60);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
ofSetColor(0, 0, 0);
ofDrawCircle(-35, 60, 15);
ofDrawCircle( 35, 60, 15);
}
発展課題2: 黒目の入ったキーポンを左右に揺らしてみてください.前出の例題使った変数 rad を利用すれば,つぎのようにプログラムできます.回転させた座標系に対して,まっすぐキーポンを描いています.(sin() の引数はラジアン(rad)が単位となり,ofRotateZ() の引数は度(deg)が単位となることに注意してください.)
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// rotate (swing)
float deg = 30 * sin(rad);
ofRotateZ(deg);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
ofSetColor(0, 0, 0);
ofDrawCircle(-35, 60, 15);
ofDrawCircle( 35, 60, 15);
}
目的とする座標系を得るためには,座標変換を段階的に積み重ねることが必要です.連続した平行移動ならば,順序を変えても同じ結果が得られます.移動量(移動ベクトル)を積算し,ひとつの ofTranslate() にまとめることも可能です.同様に,連続した回転も,順序を変えても結果は変わらず,また回転量を積算し,ひとつの ofRotateZ() にまとめることが可能です.連続した拡大縮小についても同様です.
一方,種類の異なる座標変換を適用するとき,その適用順序を変えると,結果も変わってきます.たとえば,座標系を平行移動 ofTranslate(0, 80) をしてから回転 ofRotateZ(60) をした場合,下図のような結果が得られます.(言葉で説明すれば「上に移動してから回転」です.)
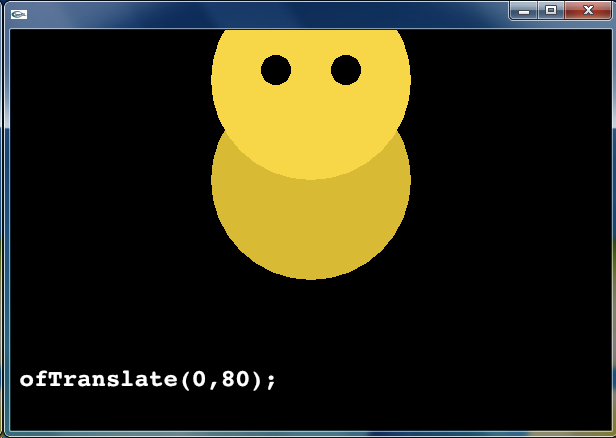
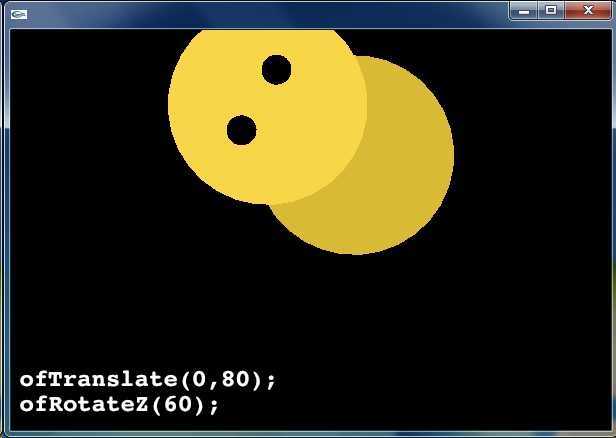
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// translate -> rotate
ofTranslate(0, 80);
ofRotateZ(60);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
ofSetColor(0, 0, 0);
ofDrawCircle(-35, 60, 15);
ofDrawCircle( 35, 60, 15);
}
逆に,平行移動 ofTranslate(0, 80) をしてから回転 ofRotateZ(60) をした場合,下図のような結果が得られます.(言葉で説明すれば「回転してから上に移動」です.) 上の例と比べると,座標変換の適用順序が異なるだけですが,得られた結果は大きく異なることに注意してください.
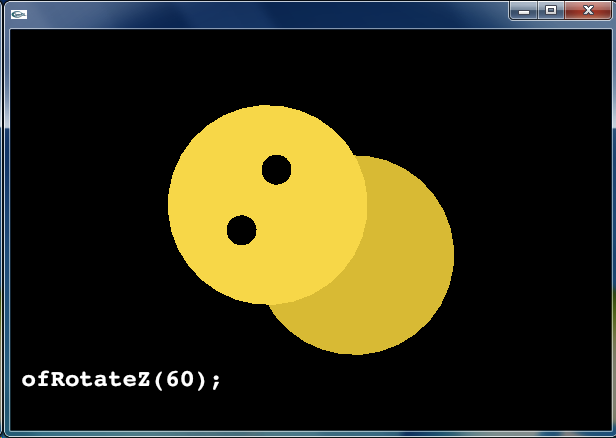
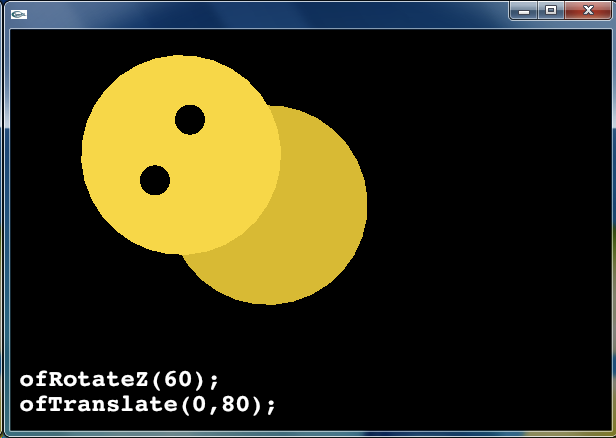
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// rotate -> translate
ofRotateZ(60);
ofTranslate(0, 80);
// keepon at origin
ofSetColor(225, 200, 50);
ofDrawCircle(0, -50, 100);
ofSetColor(250, 225, 75);
ofDrawCircle(0, 50, 100);
ofSetColor(0, 0, 0);
ofDrawCircle(-35, 60, 15);
ofDrawCircle( 35, 60, 15);
}
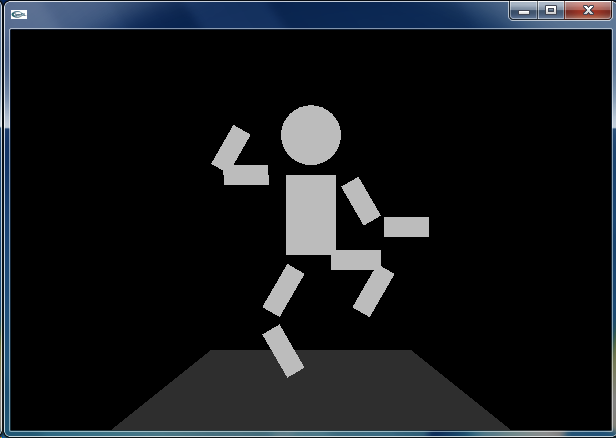
少しだけ複雑な2次元グラフィクスのアプリケーションをつくります.ofDrawRectangle() や ofDrawCircle() などで人形のカタチをつくり,それを踊らせます.まずは,emptyExample をコピーして,dojoExample5 を作ってください.
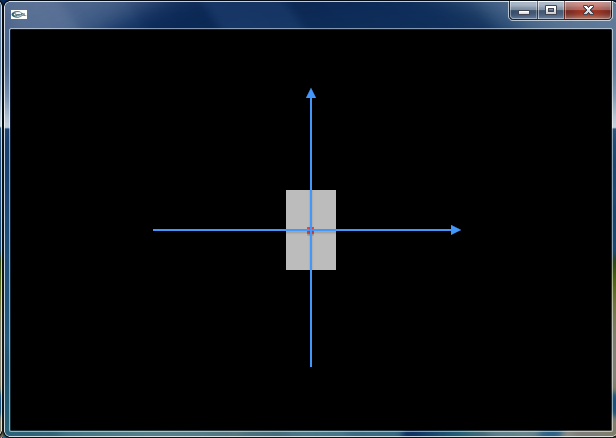
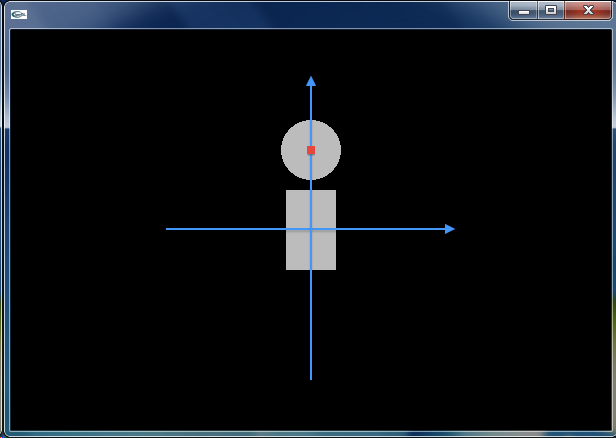
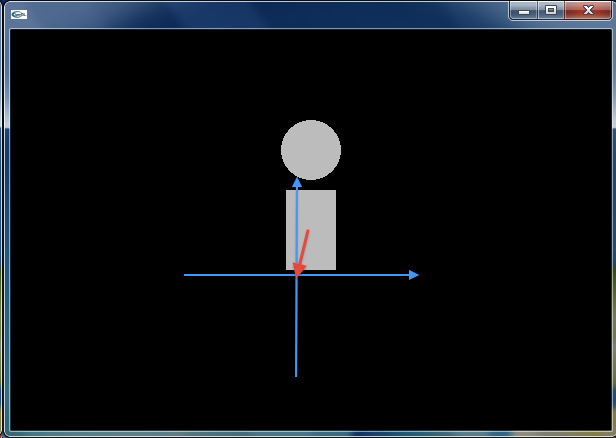
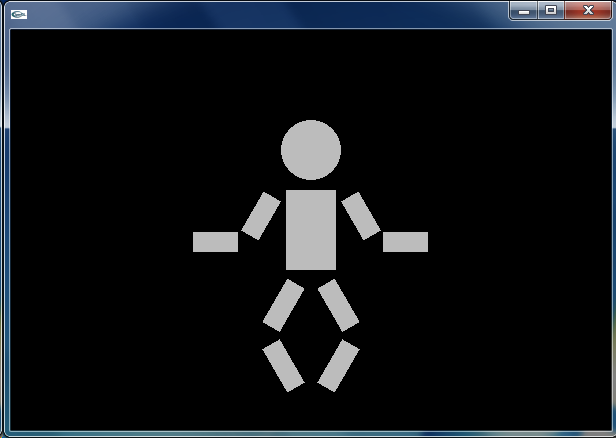
座標系を平行移動あるいは回転させ,その位置に ofDrawRectangle() や ofDrawCircle() を配置していきます.ここでは ofSetRectMode() によって,ofDrawRectangle() を,中心座標と幅・高さを指定して長方形を描画するモード (OF_RECTMODE_CENTER) にしています.デフォルトは,対角をなす2つの頂点の座標を与えるモード (OF_RECTMODE_CORNER) です.
#include "ofApp.h"
void ofApp::setup () {
ofSetWindowShape(600, 400);
ofSetFrameRate(30);
ofSetCircleResolution(32);
ofSetRectMode(OF_RECTMODE_CENTER);
ofSetBackgroundColor(0, 0, 0);
}
void ofApp::update () {
}
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// color (light gray)
ofSetColor(200, 200, 200);
//
// body
ofDrawRectangle(0, 0, 50, 80);
// head
ofDrawCircle(0, 80, 30);
// left leg (upper/lower)
ofPushMatrix();
ofTranslate(-10, -45);
ofRotateZ(-30);
ofDrawRectangle(0, -35, 20, 50);
ofTranslate(0, -70);
ofRotateZ(60);
ofDrawRectangle(0, -35, 20, 50);
ofPopMatrix();
// right leg (upper/lower)
ofPushMatrix();
ofTranslate(10, -45);
ofRotateZ(30);
ofDrawRectangle(0, -35, 20, 50);
ofTranslate(0, -70);
ofRotateZ(-60);
ofDrawRectangle(0, -35, 20, 50);
ofPopMatrix();
// left arm (upper/lower)
ofPushMatrix();
ofTranslate(-35, 40);
ofRotateZ(-30);
ofDrawRectangle(0, -30, 20, 45);
ofTranslate(0, -60);
ofRotateZ(-60);
ofDrawRectangle(0, -30, 20, 45);
ofPopMatrix();
// right arm (upper/lower)
ofPushMatrix();
ofTranslate(35, 40);
ofRotateZ(30);
ofDrawRectangle(0, -30, 20, 45);
ofTranslate(0, -60);
ofRotateZ(60);
ofDrawRectangle(0, -30, 20, 45);
ofPopMatrix();
}
注意して見てもらいたいのが ofPushMatrix() と ofPopMatrix() です.これらに挟まれた部分(字下げされた部分)での座標系への操作(平行移動・回転・スケール変換)は,その外部に影響を与えません.この例題プログラムでは,ofPushMatrix() と ofPopMatrix() で挟まれた部分を抜けると,元の座標系(胴体中心が原点)に戻ります.
では,ofPushMatrix() と ofPopMatrix() で挟まれた内部では,どのような処理をしているのでしょうか.左足を描画する部分を例として詳しく見てみましょう.
// left leg (upper/lower)
ofPushMatrix();
ofTranslate(-10, -45); // (1)
ofRotateZ(-30); // (2)
ofDrawRectangle(0, -35, 20, 50); // (3)
ofTranslate(0, -70); // (4)
ofRotateZ(60); // (5)
ofDrawRectangle(0, -35, 20, 50); // (6)
ofPopMatrix();
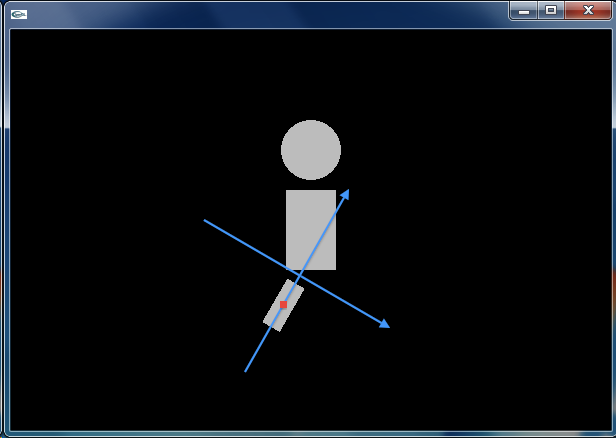
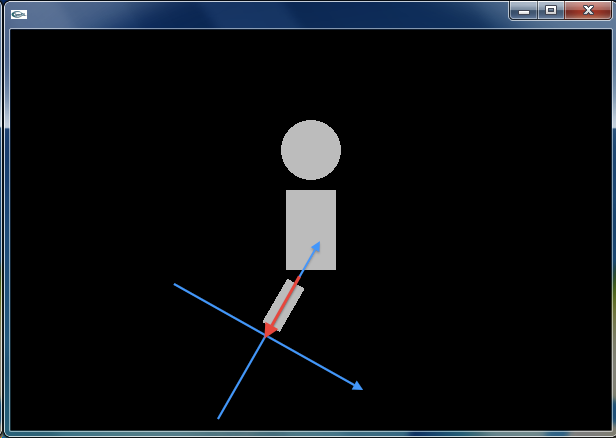
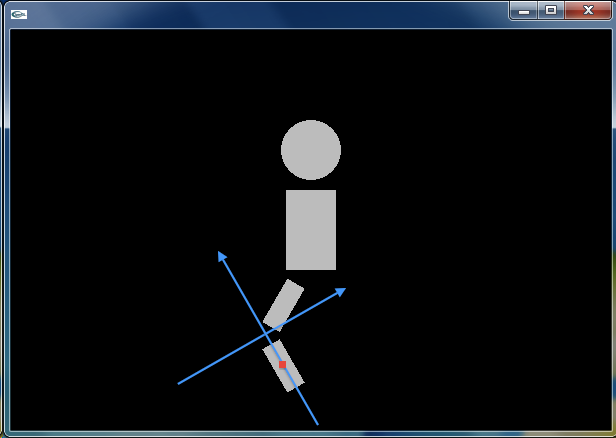
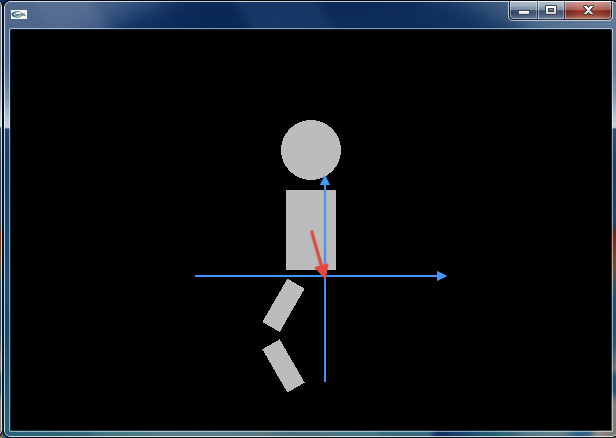
まず,この外側の座標系(標準座標系)を,左足のつけ根(胴体の左下)に (1) 平行移動させます.さらに −30deg だけ座標系を (2) 回転させます.これは股関節の回転にあたります.得られた座標系の中で,(0, -35) の位置にフトモモとなる (3) 長方形を配置します.座標系を (0, -70) の位置に (4) 平行移動し,その座標系を 60deg だけ (5) 回転させます.これは膝関節の回転にあたります.こうして得られた座標系の中で,(0, -35) の位置にスネとなる (6) 長方形を配置しています.
発展課題: このままでは人形が宙に浮いているようなので,人形が立つ舞台をつくります.奥行感のある台形の舞台です.残念ながら openFrameworks では台形を直接描画する関数が用意されていません.そこで,ofVertex() を並べて頂点列を与え,それを ofBeginShape() と ofEndShape() で囲むことで,閉じたポリゴン(多角形)を生成します.デフォルトでは,こうして生成されたポリゴンも前景色で塗りつぶされます.
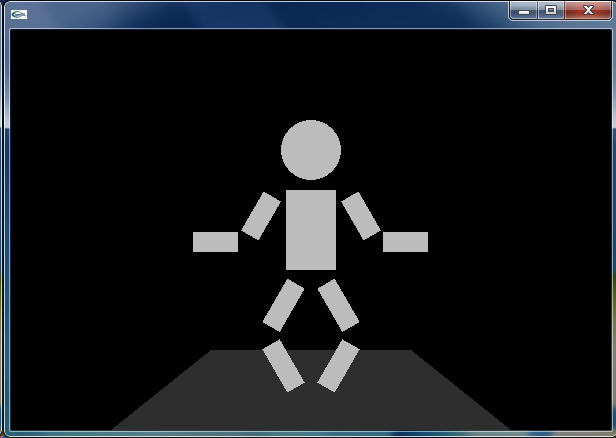
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// ground
ofSetColor(60, 60, 60);
ofBeginShape();
ofVertex(-200, -200);
ofVertex(-100, -120);
ofVertex( 100, -120);
ofVertex( 200, -200);
ofVertex(-200, -200);
ofEndShape();
// color
ofSetColor(200, 200, 200);
//
// body
(... 以下変更なし ...)
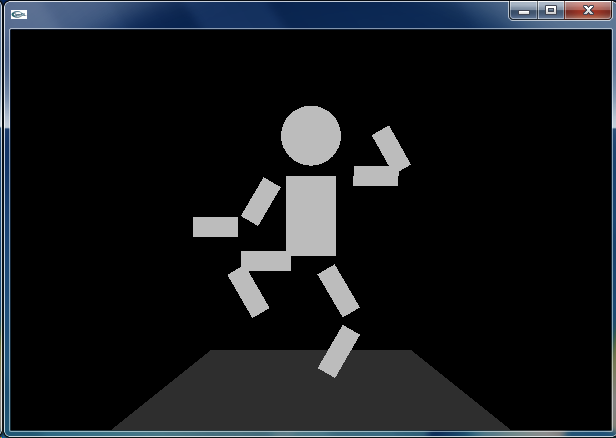
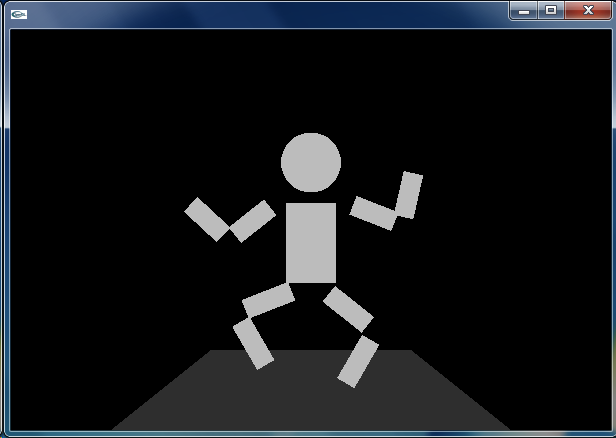
人形の手足を動かして踊らせてみます.駆動力となるのは正弦関数 sin() です.引数として与える rad を少しずつ増加させ,正弦波を作り出します.この正弦波を利用して,左足(股関節・膝関節)の角度 degLLeg,右足(股関節・膝関節)の角度 degRLeg,そして左腕(肩関節・肘関節)の角度 degLArm,右腕(肩関節・肘関節)の角度 degRArm をある範囲で振動させます.また,身体全体の垂直位置を表わす movBody も,この正弦波を利用して振動させます.
class ofApp : public ofBaseApp {
private:
float rad;
float degLLeg, degRLeg, degLArm, degRArm;
float movBody;
public:
(... 変更なし ...)
};
void ofApp::setup () {
(... 変更なし ...)
// init vars
rad = 0;
degLLeg = degRLeg = 0;
degLArm = degRArm = 0;
movBody = 0;
}
void ofApp::update () {
float s = sin(rad);
degLLeg = 30 + 30 * s;
degRLeg = 30 - 30 * s;
degLArm = 30 - 30 * s;
degRArm = 30 + 30 * s;
movBody = 15 * sin(rad * 2 - HALF_PI);
rad += 0.1;
}
void ofApp::draw () {
// setup standard coordinate system
ofTranslate(300, 200);
ofScale(1, -1);
// ground
ofSetColor(60, 60, 60);
ofBeginShape();
ofVertex(-200, -200);
ofVertex(-100, -120);
ofVertex( 100, -120);
ofVertex( 200, -200);
ofVertex(-200, -200);
ofEndShape();
// color
ofSetColor(200, 200, 200);
// move all up/down
ofTranslate(0, movBody);
//
// body
ofDrawRectangle(0, 0, 50, 80);
// head
ofDrawCircle(0, 80, 30);
// left leg (upper/lower)
ofPushMatrix();
ofTranslate(-10, -45);
ofRotateZ(-(30 + degLLeg));
ofDrawRectangle(0, -35, 20, 50);
ofTranslate(0, -70);
ofRotateZ(60 + degLLeg);
ofDrawRectangle(0, -35, 20, 50);
ofPopMatrix();
// right leg (upper/lower)
ofPushMatrix();
ofTranslate(10, -45);
ofRotateZ(30 + degRLeg);
ofDrawRectangle(0, -35, 20, 50);
ofTranslate(0, -70);
ofRotateZ(-(60 + degRLeg));
ofDrawRectangle(0, -35, 20, 50);
ofPopMatrix();
// left arm (upper/lower)
ofPushMatrix();
ofTranslate(-35, 40);
ofRotateZ(-(30 + degLArm));
ofDrawRectangle(0, -30, 20, 45);
ofTranslate(0, -60);
ofRotateZ(-(60 + degLArm));
ofDrawRectangle(0, -30, 20, 45);
ofPopMatrix();
// right arm (upper/lower)
ofPushMatrix();
ofTranslate(35, 40);
ofRotateZ(30 + degRArm);
ofDrawRectangle(0, -30, 20, 45);
ofTranslate(0, -60);
ofRotateZ(60 + degRArm);
ofDrawRectangle(0, -30, 20, 45);
ofPopMatrix();
}
発展課題: 人形は踊りましたか.周期や位相を変えることで,複雑な踊りをつくることができます.また,ここでは股関節と膝関節には同じ動きを与えていますし,肩関節と肘関節にも同じ動きを与えていますが,これらを独立に制御することで,より複雑な踊りをつくりだすことができます.チャレンジしてみてください.
最後にオマケとして,マウスをクリックすることでリズムを与えて,人形を踊らせるように改造してみましょう.ここでは,最も新しい3回分のタップ時刻 msec1, msec2, msec3 を記録し,それらの間隔から,人形が踊る周期 interval を計算しています.interval の初期値は 1000msec です.
class ofApp : public ofBaseApp {
private:
float rad;
float degLLeg, degRLeg, degLArm, degRArm;
float movBody;
int msec1, msec2, msec3;
float interval;
public:
(... 変更なし ...)
};
void ofApp::setup () {
(... 変更なし ...)
// init vars
rad = 0;
degLLeg = degRLeg = 0;
degLArm = degRArm = 0;
movBody = 0;
msec1 = msec2 = msec3 = 0;
interval = 1000;
}
void ofApp::update () {
float s = sin(rad);
degLLeg = 30 + 30 * s;
degRLeg = 30 - 30 * s;
degLArm = 30 - 30 * s;
degRArm = 30 + 30 * s;
movBody = 15 * sin(rad * 2 - HALF_PI);
rad += 0.5 * 1000 / interval * TWO_PI / 30;
}
void ofApp::draw () {
(... 変更なし ...)
}
void ofApp::mousePressed (int x, int y, int button) {
// update time stamps
msec1 = msec2;
msec2 = msec3;
msec3 = ofGetElapsedTimeMillis();
// if consistent, update interval
float inter12 = msec2 - msec1;
float inter23 = msec3 - msec2;
float mean = (inter12 + inter23) / 2;
if (abs(inter12 - inter23) / mean < 0.1) interval = mean;
}
マウスクリックによって呼び出される ofApp::mousePressed() は,まず古いクリック時刻の記録を押し出し,現在の時刻(起動時からの経過時間 [ms])を ofGetElapsedTimeMillis() によって読み出して msec3 に記録します.時間間隔 inter12, inter23 を計算し,それらの差を平均と比べて 10% 未満であれば,interval を更新しています.
ここでは,上で取り上げた「踊る人形」を素材として,それをクラス化し,そこからインスタンスを1つ生成することで,まずは同じ結果を得るようにします.つぎに,複数のインスタンス生成することで,踊る人形の集団をつくります.これらをとおして,クラスの定義方法やインスタンスの生成方法をマスターしてください.
たとえば「本」のクラスとは,さまざまな本に共通する性質をまとめたものと考えばよいでしょう.マンガから哲学書まで,さまざまな本に共通した属性(変数)として,著者名・タイトル・出版社・ページ数などが考えられます.また,可能な行為(メソッド)として,ページを開くこと,ある行を読むこと,あるページのコピーを取ること,本を閉じることなどが共通しています.さらに,紙で出来ていること,インクで文字や図形が描かれていることなど,より上位クラスである「印刷物」の性質等を受け継いでいます.
一方,個々の本は,「本」クラスの具体例であり,インスタンスと呼ばれます.クラスは設計図のようなもので,それを具体化したもの(つまり著者名・タイトルなどを設定したもの)が個々のインスタンスとなります.実体をもつインスタンスについて,ページを開くこと,ある行を読むことなど,「本」に対する行為(そして「印刷物」一般に対する行為)が可能になります.
もう少し直観的なイメージを語れば,クラスとは表をつくるゴム印のようなものです.たとえば「本」クラスであれば,下図(左側)のような感じでしょうか.ゴム印には,変数名やメソッド名が,表のように並べられています.
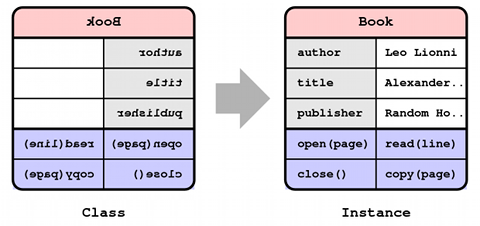
このゴム印をメモリ上に押すと,上図(右側)のようなメモリ領域が確保されます.このメモリ領域がインスタンスです.変数の値を格納する領域(白ヌキ部分)に具体的な値(数値や文字列など)を書き込むことで,1冊の本として具体的な操作(ページを開くなど)が可能になります.
それでは実際にクラス(ゴム印)を作成してみます.クラスの定義は,ゴム印そのものとなるヘッダファイル(拡張子 .h)と,メソッドごとの具体的な動作を記述したインプリメンテーション ファイル(拡張子 .cpp)によって行ないます.たとえば「踊る人形」を Dancer クラスとしてクラス化するならば,Dancer.h と Dancer.cpp によって定義することになります.
Dancer.h と Dancer.cpp をつくるには,プロジェクト > 新しい項目の追加...(Add New Item...)を開き,「C++ ファイル (.cpp)」を選択し,名前を Dancer.cpp,場所を src として「追加」を押します.同様に「ヘッダ ファイル」を Dancer.h として src に追加します.(ソリューションエクスプローラー上で src の中に Dancer.cpp と Dancer.h が新規作成されたはずです.)
Mac + Xcode の場合: Xcode 上で File > New File... を開き,ターゲットを Mac OS X の "C and C++" として,"C++ File" を選んで,"Next" を押してください.ファイル名を Dancer.cpp とし,ヘッダファイル Dancer.h も生成されるようにチェックを入れて,Finish を押してください.これで Dancer.cpp と Dancer.h が src の中に生成されたはずです.
ヘッダファイル Dancer.h は,"ofMain.h" をインクルードしたのち,class Dancer {...}; という形になります.最後にセミコロンがつくことに注意してください.先頭の "#pragma once" は,このヘッダファイルを複数回読み込まないようにするオマジナイです.括弧で囲まれた部分 {...} には,内部変数の宣言(個々のインスタンスごとに保持する変数の宣言)やメソッド(関数)のプロトタイプ宣言を並べます.private: に続く部分には,内部のみで利用する変数・メソッドを,public: に続く部分には,外部からアクセスできる内部変数・メソッドを宣言します.
たとえば,Dancer クラスの利用者は,個々のインスタンスについて private な内部変数・メソッドを直接参照することはできませんが,public な内部変数・メソッドにアクセスすることができます.private な内部変数へのアクセスは,セッタ(setter)やゲッタ(getter)と呼ばれる public メソッドを用意し,外部からのアクセスはそれらセッタ・ゲッタのみをとおして可能にすることをオススメします.ちなみに setColor() などはセッタ (setter) のよい例です.ここには例示していませんが,たとえば float getPeriod() のようなゲッタを用意することも考えられます.
#pragma once
#include "ofMain.h"
class Dancer {
private:
float posX, posY, scaleXY; // position, scale
int colorR, colorG, colorB; // skin color
float rad; // dancing phase
float period, range; // dancing period/range
float degLLeg, degRLeg, // leg posture
degLArm, degRArm; // arm posture
float movBody; // body (up/down)
public:
void setup(); // setup
void update(); // update
void draw(); // draw
void setPosition(float x, float y); // set position
void setScale(float scale); // set scale
void setColor(int r, int g, int b); // set skin color
void setPeriod(float msec); // set dancing period
void setRange(float deg); // set dancing range
};
インプリメンテーションファイル Dancer.cpp では,"Dancer.h" をインクルードしたのち,このヘッダファイルに宣言したメソッドの本体,つまり関数定義を並べていきます.openFrameworks では,setup(), update(), draw() という3つの基本メソッドと,内部変数のセッタ(setPeriod() など)やゲッタを用意するとわかりやすいでしょう.必要に応じてその他のメソッド(たとえば walk(), sleep() など)を追加してください.
#include "Dancer.h"
void Dancer::setup () {
// init with default values
posX = 0; posY = 0; scaleXY = 1;
colorR = 200; colorG = 200; colorB = 200;
period = 1000; range = 30;
rad = 0;
degLLeg = degRLeg = 0;
degLArm = degRArm = 0;
movBody = 0;
}
void Dancer::setColor (int r, int g, int b) {
// set skin color (200, 200, 200)
colorR = r; colorG = g; colorB = b;
}
void Dancer::setPeriod (float msec) {
// set period (1000)
period = msec;
}
void Dancer::setRange (float deg) {
// set range of motion (30)
range = deg;
}
void Dancer::setPosition (float x, float y) {
// set position (0, 0)
posX = x; posY = y;
}
void Dancer::setScale (float scale) {
// set scale (1)
scaleXY = scale;
}
void Dancer::update () {
// update posture
float s = sin(rad);
degLLeg = 30 + range * s;
degRLeg = 30 - range * s;
degLArm = 30 - range * s;
degRArm = 30 + range * s;
movBody = 15 * sin(rad * 2 - HALF_PI);
// increment the phase
rad += 0.5 * 1000 / period * TWO_PI / 30;
}
void Dancer::draw () {
// begin (encapsulation)
ofPushMatrix();
ofPushStyle();
ofSetCircleResolution(32);
ofSetRectMode(OF_RECTMODE_CENTER);
// position/scale
ofTranslate(posX, posY);
ofScale(scaleXY, scaleXY);
// color
ofSetColor(colorR, colorG, colorB);
// body
ofTranslate(0, movBody);
ofDrawRectangle(0, 0, 50, 80);
// head
ofPushMatrix();
ofTranslate(0, 80);
ofDrawCircle(0, 0, 30);
ofPopMatrix();
// left leg (upper/lower)
ofPushMatrix();
ofTranslate(-10, -45);
ofRotateZ(-(30 + degLLeg));
ofTranslate(0, -35);
ofDrawRectangle(0, 0, 20, 50);
ofTranslate(0, -35);
ofRotateZ(60 + degLLeg);
ofTranslate(0, -35);
ofDrawRectangle(0, 0, 20, 50);
ofPopMatrix();
// right leg (upper/lower)
ofPushMatrix();
ofTranslate(10, -45);
ofRotateZ(30 + degRLeg);
ofTranslate(0, -35);
ofDrawRectangle(0, 0, 20, 50);
ofTranslate(0, -35);
ofRotateZ(-(60 + degRLeg));
ofTranslate(0, -35);
ofDrawRectangle(0, 0, 20, 50);
ofPopMatrix();
// left arm (upper/lower)
ofPushMatrix();
ofTranslate(-35, 40);
ofRotateZ(-(30 + degLArm));
ofTranslate(0, -30);
ofDrawRectangle(0, 0, 20, 45);
ofTranslate(0, -30);
ofRotateZ(-(60 + degLArm));
ofTranslate(0, -30);
ofDrawRectangle(0, 0, 20, 45);
ofPopMatrix();
// right arm (upper/lower)
ofPushMatrix();
ofTranslate(35, 40);
ofRotateZ(30 + degRArm);
ofTranslate(0, -30);
ofDrawRectangle(0, 0, 20, 45);
ofTranslate(0, -30);
ofRotateZ(60 + degRArm);
ofTranslate(0, -30);
ofDrawRectangle(0, 0, 20, 45);
ofPopMatrix();
// end (restoration)
ofPopStyle();
ofPopMatrix();
}
Dancer::draw() の中では,最初に ofPushMatrix() / ofPushStyle(),最後に ofPopStyle() / ofPopMatrix() を呼び出しています.これは,Dancer::draw() による「踊る人形」の描画が,それ以外のグラフィック描画に影響を与えないようにするためです.ofPushMatrix() / ofPopMatrix() は座標変換について,ofPushStyle() / ofPopStyle() は色や線幅の操作について,影響範囲を限定してくれます.
Dancer クラスが用意できたら,つぎに ofApp の中で Dancer クラスのインスタンスを生成し,それを踊らせてみましょう.
まず,ofApp.h の中で,"Dancer.h" をインクルードするようにします.これで Dancer クラスを利用できるようになります.つぎに,private 変数として,Dancer クラスの変数(つまり Dancer クラスのインスタンス)dancer を生成(つまりゴム印を押してメモリ領域を確保)するようにします.
#pragma once #include "ofMain.h" #include "Dancer.h" class ofApp : public ofBaseApp{ private: Dancer dancer; public: void setup(); void update(); void draw(); void keyPressed(int key); void keyReleased(int key); void mouseMoved(int x, int y); void mouseDragged(int x, int y, int button); void mousePressed(int x, int y, int button); void mouseReleased(int x, int y, int button); void windowResized(int w, int h); void dragEvent(ofDragInfo dragInfo); void gotMessage(ofMessage msg); };
#include "ofApp.h"
void ofApp::setup () {
ofSetWindowShape(600, 400);
ofSetFrameRate(30);
ofSetCircleResolution(32);
ofSetRectMode(OF_RECTMODE_CENTER);
ofSetBackgroundColor(0, 0, 0);
// dancer
dancer.setup();
}
void ofApp::update () {
dancer.update();
}
void ofApp::draw () {
ofTranslate(300, 200);
ofScale(1, -1);
dancer.draw();
}
void ofApp::mousePressed (int x, int y, int button) {
}
(... 以下変更なし ...)
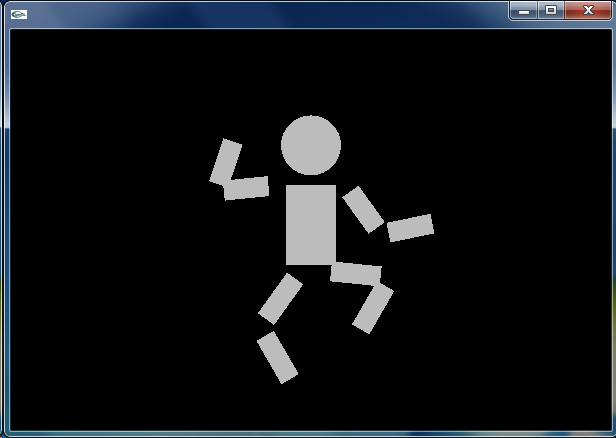
ofApp.cpp の中では,インスタンス dancer について,dancer.setup() を呼び出すことで初期化し,ofApp::update() の中では dancer.update() を呼び出し,ofApp::draw() の中では dancer.draw() を呼び出すことで,dancer を描画しています.ビルドし実行すると,右上図のように,前出の「踊る人形」と同じような結果が得られるはずです.
クラスはインスタンスの設計図をゴム印にしたものと考えられます.メモリ上にこのゴム印を押すことで,インスタンスを生成し,それを利用することができます.そのメリットのひとつは,1つのクラスから複数個のインスタンスを簡単に生成できることです.あるいは「クラスを再利用すること」と言い換えてもよいでしょう.
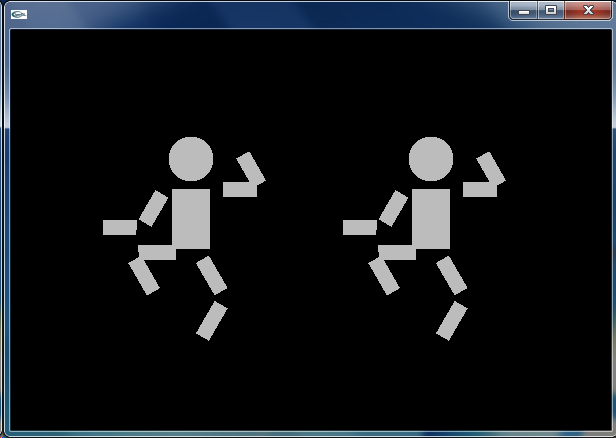
上のプログラムを,つぎのように変更してみてください.2つの(小さめの)人形が,同期して踊るはずです.
#pragma once
#include "ofMain.h"
#include "Dancer.h"
class ofApp : public ofBaseApp {
private:
Dancer dancer1, dancer2;
public:
(... 変更なし ...)
};
#include "ofApp.h"
void ofApp::setup() {
ofSetWindowShape(600, 400);
ofSetFrameRate(30);
ofSetCircleResolution(32);
ofSetRectMode(OF_RECTMODE_CENTER);
ofSetBackgroundColor(0, 0, 0);
// dancer1
dancer1.setup();
dancer1.setPosition(0, -120);
dancer1.setScale(0.75);
// dancer2
dancer2.setup();
dancer2.setPosition(0, 120);
dancer2.setScale(0.75);
}
void ofApp::update() {
dancer1.update();
dancer2.update();
}
void ofApp::draw() {
ofTranslate(300, 200);
ofScale(1, -1);
dancer1.draw();
dancer2.draw();
}
(... 以下変更なし ...)
発展課題: これが出来たら,ofApp::setup() の中で,setPeriod() によって,dancer1 には 900 [ms],dancer2 には 800 [ms] の周期を与えてみてください.また,setRange() によって動きの大きさ(30deg が標準)を変えてみてください.どのような踊りになるでしょうか.
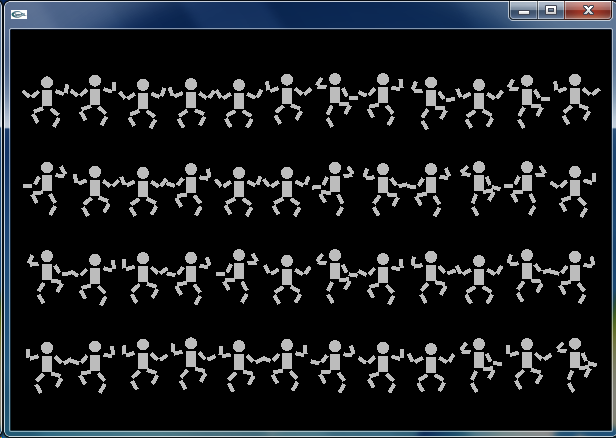
48個の人形を,それぞれランダムに与えた周期と動作の大きさで踊らせてみましょう.これだけの個数になると,dancer1, dancer2, ... のような個別のインスタンス変数として扱うのは面倒です.そこで配列(インスタンスの配列)を利用します.
#pragma once #include "ofMain.h" #define DANCERS 48 #include "Dancer.h" class ofApp : public ofBaseApp { private: Dancer dancers[DANCERS]; public: (... 変更なし ...) };
#include "ofApp.h"
void ofApp::setup() {
ofSetWindowShape(600, 400);
ofSetFrameRate(30);
ofSetCircleResolution(32);
ofSetRectMode(OF_RECTMODE_CENTER);
ofSetBackgroundColor(0, 0, 0);
// OZS 48
for (int i = 0; i < DANCERS; i++) {
dancers[i].setup();
dancers[i].setScale(0.2);
dancers[i].setPeriod(ofRandom(500, 1000));
dancers[i].setRange(ofRandom(10, 40));
dancers[i].setPosition(((i % 12) - 5.5) * 48,
((i / 12) - 1.5) * 88 );
}
}
void ofApp::update() {
for (int i = 0; i < DANCERS; i++)
dancers[i].update();
}
void ofApp::draw() {
ofTranslate(300, 200);
ofScale(1, -1);
for (int i = 0; i < DANCERS; i++)
dancers[i].draw();
}
(... 以下変更なし ...)
ofApp::setup() に登場した ofRandom(min, max) は,openFrameworks によって提供される乱数発生器です.min から max までの乱数(float)を返します.(ofRandom(max) は 0 から max までの乱数(float)を返します.)
これをビルドし実行すると,左図のように,48個の人形がそれぞれの周期と動作の大きさで踊り出します.ひとたび内部変数(period, range など)を設定すれば,あとは update() と draw() を呼び出すことで,それぞれの人形は自律的に踊ることができます.ひとつひとつの人形が生きているかのように見えませんか.
