ギヤ（減速機）・ブラシつきDCモータ・エンコーダを組み合わせたアクチュエータの動きをシミュレートすることを考えます．ここでは例題として，アクチュエータの出力軸に〈棒〉を取り付け，その棒の一端に〈おもり〉をつけた系を想定します．アクチュエータを水平に固定して，この〈おもり〉つきの〈棒〉の角度（位置）を制御するというものです．ロボットの〈腕〉のようなものを想像してください．

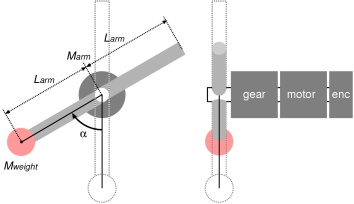
〈棒〉は質量 M_arm [kg]，長さ 2L_arm [m] の均一な細棒（線）とし，その中央で回転するものとします．〈おもり〉は質量 M_weight の小球（質点）とします．この系の慣性モーメント J_load はつぎのようになります．

また，〈腕〉の回転角度を α [rad] で表わし，重力方向に下がっているときの角度を 0，時計回り（CW）を正方向とすると，この角度に〈腕〉を保持するために必要なトルク T_load はつぎのようになります．（ここで g を重力加速度 9.8 [m/s²] とします.）

ここでいう CW 方向とは，モータ（とエンコーダ）における正方向のことです．多くの場合，モータ単体を出力軸側から見たとき，時計回りの方向になります．遊星ギヤならば，ギヤの出力軸とモータの出力軸は同じ方向に回ります．ハーモニック=ドライブの場合は，反対方向になるでしょう．

市販のモータには，電気的および機械的な特性データが（モータ添付あるいはウェブ上で）提供されています．モータを選定する上では，定格トルク [Nm]・定格出力 [W] などが重要ですが，モータ制御をシミュレートする上では，以下のデータが重要になります．

• 定格電圧 V_o [V]
  ふつう「12V のモータ」と呼ばれるモータは 12V が定格電圧です．これはモータに印加できる最大電圧ではありません．短時間なら，定格の２倍の電圧をかけることもありえます．
• 無負荷回転速度 ω_o [rad/s]
  無負荷のモータに定格電圧 V_o を印加して，最高回転数に達したときの角速度です．特性データには rpm（毎分回転数）で表示されるとが多いのですが，シミュレーションには rad/s （= rpm × 2π ⁄ 60）に変換して使います．
• 無負荷電流 I_o [A]
  無負荷のモータに定格電圧 V_o を印加して，最高速度ω_o に達したときにモータを流れる電流です．起動時（速度 0 のとき）に流れる電流と比べると，かなり小さな値となります．
• 巻線抵抗 R [Ω]
  モータの巻線がもつ直流抵抗値です．定格電圧 V_o でモータをスタートさせたとき，起動時に流れる電流 I_s は，V_o ⁄ R のように計算できます．
• トルク定数 K_M [Nm/A]
  DCモータは，モータを流れる電流 I に比例したトルク T_mot を発生させます．この比例定数が K_M で，T_mot = K_M I となります．定格電圧 V_o でモータをスタートさせたとき，起動時のトルク T_s は，K_M I_s = K_M V_o ⁄ R のように計算できます．また，最高速度 ω_o で安定しているときでも無負荷電流 I_o が流れるのは，この電流によって発生するトルク K_M I_o がモータ内部の摩擦抵抗に打ち消されているためです．
• 逆起電力定数 K_e [V/ω]
  モータは電源によって回されながら，同時に発電機として〈発電〉しているため，回転速度 ω に比例した逆電位差e がモータ端子に発生します．逆起電力定数 K_e はこの比例定数で，e = K_e ω となります．K_e [V/ω] は，トルク定数 K_M [Nm/A] と同じ値になるため，特性データに記述されないことが多いようです．
• ロータ慣性モーメント J_mot [kgm²]
  モータのロータ（回転子）のもつ慣性モーメントです．J_mot が大きなモータは加減速に時間がかかります．本シミュレーションで想定している「コアレス=モータ」は，回転子に鉄心を持たないため，J_mot を低く抑えています．

これら特性データから，モータ端子に電圧 V を与えたときのモータの挙動をつぎのように計算（シミュレート）できます．まず，モータに流れる電流I は，現在のモータ回転速度を ω とすると，逆起電力による電位差 K_e ω を差し引いた電圧がロータ巻線に印加されるので，

となります．このときモータが発生させるトルク T_mot は，ブラシや軸受による摩擦抵抗も考慮すれば，

となります．摩擦係数 B は，本来トルクを必要としない無負荷回転速度 ω_o での定常運転時に無負荷電流I_o が流れることから，B = K_M I_o / ω_o と求めることができます．

一方，ギヤ（減速機）については，以下のような機械的な特性データが（ギヤ添付あるいはウェブ上で）提供されています．（ギヤを選定するときには，このほかに，負荷に合った許容トルク（連続・瞬間）を考慮する必要があります.）

• 減速比 ρ
  入力側（モータ側）が何回転すれば出力側が１回転するのかを表わした数です．たとえば減速比 100 ならば，モータを 100 回転させると，出力軸が１回転することになります．
• 伝達効率 η
  モータから入力されるエネルギーのうち，ギヤから出力されるエネルギーの割合（0〜1）です．伝達されないエネルギーは熱などに変わります．ここでは便宜上，入力トルクを T_in，出力トルクを T_out とするとき，T_out = ηρT_in になると考えます．
• ギヤ慣性モーメント J_gear [kgm²]
  入力側（モータ側）からみたギヤの慣性モーメントです．

ギヤや負荷がつながれた状態で，モータがトルク T_mot を発生させた場合，モータの角加速度 ω' はつぎのように計算できます．

分子にくる T_mot − T_load ⁄ (ηρ) は，モータが発生させるトルク T_mot から，負荷を駆動（あるいは保持）するために必要なトルク T_load ⁄ ηρ を引いたもので，系全体を動かすトルクとなります．負荷トルク T_load は，一般には上の例題のように，α ( = ∫ ω ⁄ρ ) の関数になるでしょう．一方，分母に来るのは，モータ側からみた系全体の慣性モーメントです．モータ側からみると，ギヤの出力側（負荷側）の慣性モーメント J_load は 1 ⁄ ρ² 倍になります．

これが，モータを含めた系全体の運動方程式になります．たとえば初期値として，時刻 t = 0 における α = 0，ω = 0，V = 0 とし，時刻 t > 0 に電圧 V をモータに印加したとすれば，微小時間ごとに角加速度 ω' を計算し，それに応じて角速度 ω を更新することで，モータの挙動をシミュレートできるわけです．

では実際に，モータの挙動をシミュレートしてみましょう．ここでは，maxon motor のブラシつきコアレスDCモータに遊星ギヤを組み合わせたアクチュエータを例として，〈腕〉の駆動シミュレーションを試みます．使用するモータ・ギヤの特性データは，メーカからつぎのように提供されています．

モータ： maxon 118637
(RE 13 φ13mm, Graphite Brushes, 3W)
Vo	12 [V]
ωo	1371.83 [rad/s]	(13100 [rpm])
Io	0.0444 [A]	(44.4 [mA])
R	9.07 [Ω]
KM	0.842×10-2 [Nm/A]	(8.42 [mNm/A])
Jmot	0.541×10-7 [kgm²]	(0.541 [gcm²])

ギヤ： maxon 110315
(Planetary Gearhead GP 13 A)
ρ	67.49	(185193 / 2744)
η	0.75	(75 [%])
Jgear	0.15×10-8 [kgm²]	(0.015 [gcm²]

モータの挙動は，微小時間（Δt_sim）ごとに，上述の運動方程式からモータの角加速度 ω' を計算し，モータの角速度 ω や回転角度 θ = ∫ ω を更新することでシミュレートできます．その手順は，およそつぎのように記述できます．（ここでは積分計算に台形近似を利用していますが，より精度を上げるには，より小さな Δt_sim でモータの挙動をシミュレートすることや，積分計算にシンプソン則（放物線による近似）やルンゲ=クッタ法などを適用することなどが考えられます.）

上にあげたモータとギヤの特性データを与え，例題にならって L_arm = 0.1 [m]，M_arm = 0.1 [kg]，M_weight = 0.1 [kg] として，sim_loop(2.0, 3.0) を呼び出してみます．横軸を時刻 t [s]，縦軸を〈腕〉の角度 α = θ ⁄ ρ [rad] として出力結果をグラフにすると，つぎのようになります．

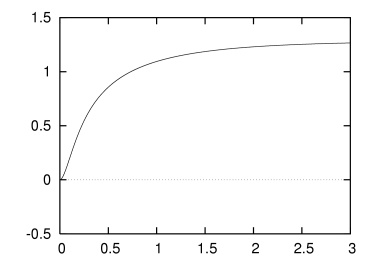
これは，〈腕〉を真っすぐ下げて静止させた状態から，モータに 2V の電圧をかけたときの α の変化を Δt_sim = 0.0001 [s] ごと に３秒間にわたってシミュレートすることにあたります．動きだした〈腕〉の角度が，モータのトルクと負荷のトルクがつりあう α = 1.27 [rad]（約73度）付近に収束していくのがわかります．

プログラムを少し変更すれば，最初の１秒間はモータに 2V の電圧をかけ，つぎの１秒間は 0V にし，最後の１秒間でまた 2V に戻した場合の挙動もシミュレートできます．下のグラフはその結果を表わしています．最初の１秒間は上の図と全く同じですが，急にパワーを失って，α = 0 付近まで戻ってくる様子がわかります．

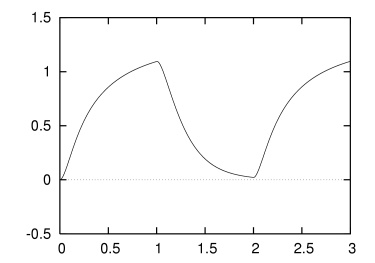
いよいよ〈腕〉の角度 α のフィードバック制御をシミュレートします．モータの回転角度 θ = ∫ ω （ただし，α = 0 のとき θ = 0）をエンコーダで読み取り，モータに印加する電圧を加減しながら，〈腕〉を希望する角度 α_goal まで ── つまりモータの回転角度をθ_goal = ρ α_goal まで ── 移動させ，その角度を保持するというものです．ここでは，制御周期 Δt_c = 0.001 [s]，つまり制御サイクル 1000 [Hz] を想定することにします．

エンコーダは，一般に，モータの回転軸に取り付けます．たとえば，シミュレーションの対象とするエンコーダは，下表のように，モータ１回転で 256 パルスの A/B 相の信号を発生させます．Pico-2 の場合，このパルスを 90 度の位相ごとに（つまり４倍にして）カウントするため，この例では 1024 カウント/回転として扱うことになります．

エンコーダ： maxon 241062
(Encoder MR, Type S, 256 pulses per turn, 2 channels)
Nenc	256 [pulses/turn]	(1024 [counts/turn])

Pico-2 はエンコーダの A/B 信号を常に積分しているため，ユーザはいつでもモータ回転軸の角度 θ を BIOS 関数 ENC_get() で読みだすことができます．ENC_get() は現在の角度（単位は count）を整数値として返すので，たとえば上のエンコーダの場合，dθ = 2π ⁄ 1024 とすると，θ = ENC_get() × dθ となります．（Pico-2 起動時のモータ回転軸の状態が θ = 0 となります.）

モータ制御の基本は，目標角度 θ_goal と現在角度 θ の誤差（error） e = θ_goal − θ にもとづいて，モータに印加する電圧 V （およびその極性）を加減するというものです．なかでも一番単純な方法は，誤差 e に比例した電圧 V をモータに印加するというもので，「比例制御（proportional control）」と呼ばれます．

ここで K_p は「比例ゲイン」と呼ばれる定数です．V の値が負のときは，モータに逆方向の電圧をかけます．V の絶対値がモータ駆動電源の電圧 V_mp を超えないことに注意してください．

たとえば V_mp = 12.0 [V] として，cont_loop(0.2, 1.0, 3.0) を呼び出してみます．これは K_p = 0.2，α_goal = 1.0 [rad] としたときの〈腕〉の挙動を３秒間シミュレーションすることにあたります．横軸を時刻 t [s]，縦軸を〈腕〉の角度 α [rad] として出力結果をグラフにすると，つぎのようになります．

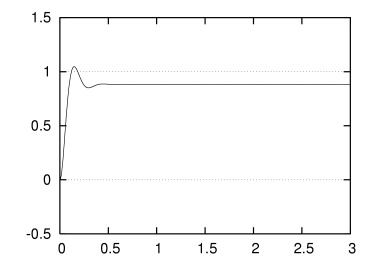
わずかに振動した後，α = 0.88 あたりに収束しているのがわかります．α_goal = 1.0 との差 e_ss によって発生する出力トルクと負荷によるトルクがつりあっている状態です．この差e_ss を「定常誤差（steady-state error）」と呼びます．

つぎに比例ゲイン K_p = 2.0 としてシミュレートしてみます．小刻みに振動しながら α = 0.987 あたりに収束し，定常誤差が小さくなっていることがわかります．

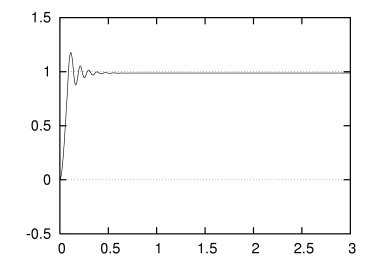
さらに比例ゲイン K_p = 20.0 まで上げてみます．小刻みな振動が収まらないのがわかります．例題のように重力に抗するような動作をさせる場合，比例制御だけで振動させずに定常誤差をなくすことは原理的に不可能です．

定常偏差をなくすために，誤差 e の積分値をモータに印加する電圧V に反映させる「積分制御（integral control）」を導入します．通常，比例制御と合わせた「比例⋅積分制御」として，つぎのように V を制御します．

ここで K_i は「積分ゲイン」と呼ばれる定数です．実際の積分計算は，離散時間 τ ごとに誤差 e(τ) を積算していきますので，つぎのようになります．

さらに，積分値が大きくなりすぎると，目標角度をつぎつぎと変えた場合の追従性が悪くなるので， | K_i Σe(τ)Δt_c | の 値が V_mp を超えない範囲に抑えます．すると比例=積分制御のプログラムは，およそつぎのようになります．

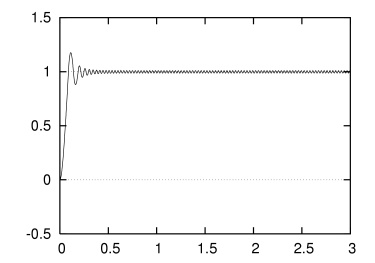
K_p = 0.2，K_i = 1.0 としてシミュレートしてみると，比例制御だけの場合には残っていた定常偏差がほぼ 0 になっているのがわかります．

つぎに振動を減らすことを考えます．バネのような性質をもった比例制御に，ダンパ（ショック=アブソーバ）のような粘性をもった「微分制御（differential control）」を導入することで，余分な振動を抑えることができます．モータに印加する電圧 V の制御は，つぎのようになります．

ここで K_d は「微分ゲイン」と呼ばれる定数で，摩擦係数のようなものと考えることができます．実際の微分は，現在の誤差を e(t)，前時刻の誤差を e(t−1) として，つぎのように求めます．

一方，このように誤差 e の微分を利用するのではなく，回転角度 θ の微分（つまり角速度）を利用した微分制御もあります．ちょうどハチミツの中でスプーンを動かしたときに，その速度に比例した抵抗を感じる「粘性」そのもので，つぎのように表わすことができます．

目標角度 α_goal が頻繁に変更されるロボット制御には，こちらの方法が適していることが多いようです．以下では，この回転角度の微分にもとづく微分制御について扱うことにします．そのプログラムは，およそつぎのようになります．

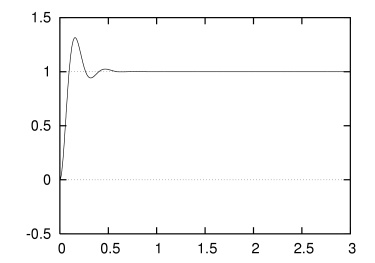
K_p = 2.0，K_d = 0.05 としてシミュレートしてみると，比例制御だけの場合に見られた余分なオーバーシュートや小刻みな振動が，微分制御の導入によって取り除かれているのがわかります．しかし，わずかながら定常偏差は残されたままになっています．

なお，微分操作を含んだ制御（比例⋅微分制御および後述する比例⋅積分⋅微分制御）では，制御周期 Δt やエンコーダ分解能 dθ の値によっては，標本化ノイズ（いわゆるエイリアシング）の影響で，出力が「ブィーン」と発振してしまうことがあります．たとえば，低い分解能のエンコーダを短い制御周期（高い制御サイクル）で使用した場合，θ の変化（つまり微分値）がスパイク状になり，大きな微分ゲイン K_d では発振してしまうでしょう．このような場合は，微分値 (θ(t) − θ(t−1)) ⁄ Δt_c そのままではなく，ローパスフィルタによって高周波成分を除去（アンチエイリアシング）したものを微分操作に使うことで解決可能です．

最後に，比例⋅積分制御による定常偏差の解消と，比例=微分制御による振動の抑制を，両方とも取り込むことにしましょう．それが「比例⋅積分⋅微分制御（PID control）」です．多くのロボットや産業機器に利用されている制御方法です．モータに印加する電圧 V は，つぎのように制御されます．

これをプログラムにすると，およそつぎのようになります．

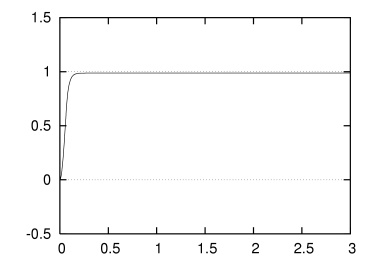
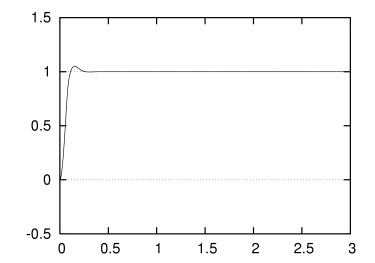
K_p = 2.0，K_i = 40.0，K_d = 0.05 としてシミュレートしてみると，定常偏差が解消され，振動もかなり抑制されていることがわかります．

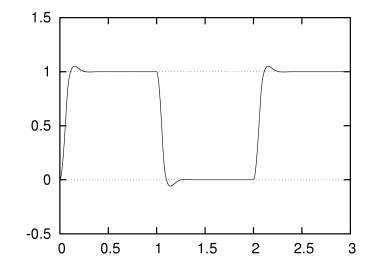
同じパラメータで，最初に１秒間は α_goal を 1 [rad] に，つぎの１秒間は 0 [rad] に，最後の１秒間はまた 1 [rad] に設定して，シミュレートしてみます．きれいな動きをみせているのがわかります．

Pico-2 でモータを制御するには，モータ・ギヤ・負荷などの特性に合った制御パラメータを設定する必要があります．そのための実践的な方法は，まずシミュレーションで最適な制御パラメータを決めて，それを実機で微調整するというものです．

制御パラメータの〈当たり〉をつけるための道具として，モータの応答をグラフで見ることができる〈PID 制御シミュレータ〉を用意しました．JavaScript で書いてあるので，対応できるブラウザであれば，そのまま利用できるはずです．

対象となるモータ・ギヤおよび負荷の特性を入力し，PIDパラメータ（K_p, K_i, K_d）と制御周期（Δt）・モータ駆動電源の電圧（V_mp）を適当に設定して，〈シミュレーション ＋ グラフ描画〉のボタンを押してください．下のグラフ領域にシミュレーション結果が表示されます．横軸は時刻 t [s]，縦軸は〈腕〉の角度 α [rad] です．このシミュレータで，望ましい応答が得られるように適切なパラメータを探索してください．

    PID 制御シミュレーション    

モータ特性 Vo V ωo rad/s Io A R Ω KM Nm/A Jmot kgm² データ Maxon 1.5W 118578 参照 Maxon 3.0W 118637 ギヤ特性 ρ η Jgear kgm² エンコーダ特性 Nenc pulses 負荷特性 Larm m Marm kg Mweight kg

PIDパラメータ Kp Ki Kd PID制御周期 Δtc s モータ駆動電源 Vmp V 制御指令 (tgoal, αgoal) 1 2 3 グラフ設定 (min/max/step) t [s] α [rad]

安定性を求めるのか，変化する目標角度への追従性を求めるのかなど，目的に応じて最適なパラメータは変わります．また，負荷に変動が少ない場合と，負荷が大きく変動する場合とでも，最適なパラメータが変わってくるでしょう．

比例ゲイン K_p を大きくしすぎると発振やオーバーシュートが目立つようになります．積分ゲイン K_i を大きくしすぎると振動してしまいます．微分ゲイン K_d を大きくしていけば発振や振動を抑えられますが，逆に応答性・追従性が悪くなるでしょう．発振しない範囲で，振動やオーバーシュートを抑えつつ応答性を高めるように，それぞれのパラメータを調整していきます．